Check out this tutorial to learn about triangles! A triangle is a special right triangle (a right triangle being any triangle that contains a 90 degree angle) that always has degree angles of 30 degrees, 60 degrees, and 90 degrees Because it is a special triangle, it also has side length values which are always in a consistent relationship with one anotherSimilarity in Right Angled Triangles 30 60 90 and 45 45 90 Theorem Circle Theorem of External Division of Chords Theorem of Internal Division of Chords Converse of Theorem of the Angle Between Tangent and Secant Theorem of Angle Between Tangent and Secant Converse If a pair of opposite angles of a quadrilateral is supplementary

30 60 90 Triangle Definition Theorem Formula Examples
When to use 30 60 90 triangle
When to use 30 60 90 triangle-30°60°90° Triangle Theorem In a 30°60°90° triangle, the hypotenuse is twice as long as the shorter leg, and the longer leg is √3 times as long as the shorter leg side opposite 30° is x, side opposite 60° x√3 and side opposite 90° is 2x30 60 90 Triangle Definition Theorem Formula Examples Section 2 2 Trig Ratios With Any Angle Ppt Download The 30 60 90 Triangle Topics In Trigonometry A Assimilation Time Frame Minutes Use The The Gauthmath 30 60 90 45 45 90 Special Right Triangles Free Printable Math Worksheets Teaching Geometry Printable Math Worksheets



1
30 60 90 triangle theorem definition If so, then your textbook will supply the formulae How to find the sides of the given triangle definition, 2 examples, and their solutions Formula A triangle is a triangle whose interior angles are 30º, 60º, and 90º The triangle is a special right triangle, and knowing it can save you a lot of time on Definition of Triangles Sides of the triangle has special properties (triangle inequality theorem) The theorem is sum of two any sides of triangles is more than the third side 2 Another special triangle is triangle that has angle 30°, 60°, and 90° It also has ratio in the sidesA triangle is a special right triangle with some very special characteristics If you have a degree triangle, you can find a missing side length without using the Pythagorean theorem!
30 60 90 Triangle Theorem Definition Triangle Midsegment Theorem The midsegment of a triangle is Triangle Inequality Theorem The sum of any two sides of a triangle is greater than the triangle's third side Pythagorean Theorem of the len Pythagorean Inequalities Theorem Triangle Theorem Triangle Theorem If all three sides of one triangle are congruent to the A triangle is a special right triangle (a right triangle being any triangle that contains a 90 degree angle) that always has degree angles of 30 degrees, 60 degrees, and 90 degrees Because it is a special triangle, it also has side length values which are always in a consistent relationship with one another 30 60 90 triangle sides If we know the shorter leg length a, we can find out that b = a√3 c = 2a If the longer leg length b is the one parameter given, then a = b√3/3 c = 2b√3/3 For hypotenuse c known, the legs formulas look as follows a = c/2
Tweet Definition of a triangle along with the ratio of its sidesAlthough all right triangles have special features – trigonometric functions and the Pythagorean theorem The most frequently studied right triangles, the special right triangles, are the 30, 60, 90 Triangles followed by the 45, 45, 90 trianglesTriangles Concept A 30 60 90 triangle is a special type of right triangle What is special about 30 60 90 triangles is that the sides of the 30 60 90 triangle always have the same ratio Therefore, if we are given one side we are able to easily find the other sides using the ratio of 12square root of three



Solve A 30 60 90 Triangle With Gradea




30 60 90 Triangle Rules Sides Ratio Of A 30 60 90 Triangle Video Lesson Transcript Study Com
Example of 30 – 60 90 rule Example 1 Find the missing side of the given triangle As it is a right triangle in which the hypotenuse is the double of one of the sides of the triangle Thus, it is called a triangle where smaller angle will be 30 The longer side is always opposite to 60° and the missing side measures 3√3 units inA triangle is a right triangle where the three interior angles measure 30 °, 60 °, and 90 ° Right triangles with interior angles are known as special right triangles Special triangles in geometry because of the powerful relationships that unfold when studying their angles and sidesA triangle is a special right triangle with some very special characteristics If you have a triangle, you can find a missing side length without using the Pythagorean theorem!




30 60 90 Triangle Theorem Ratio Formula Video
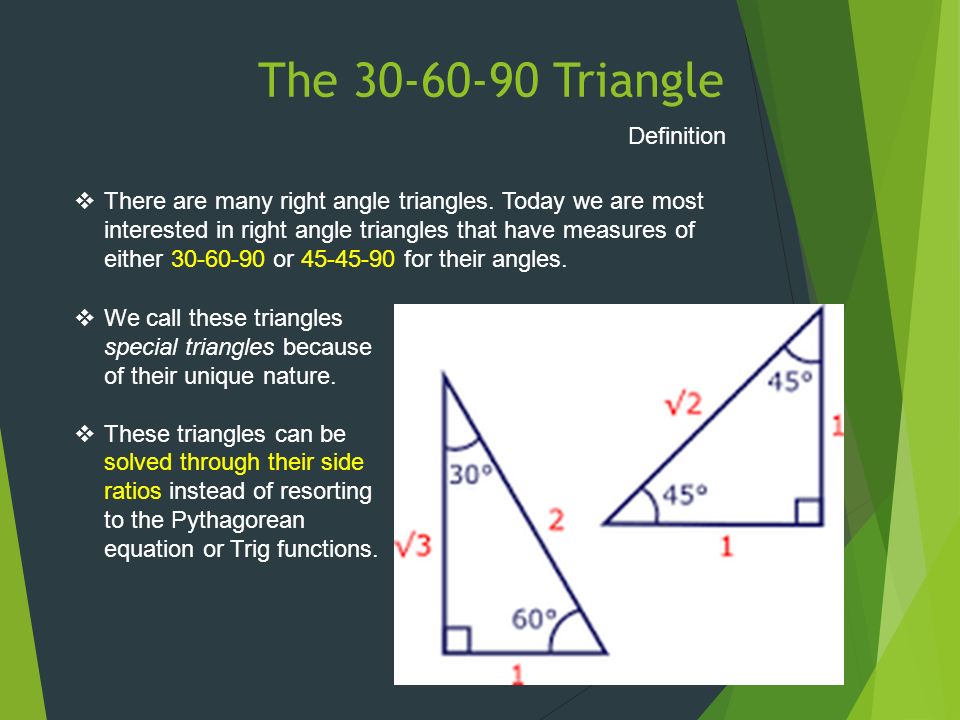



Special Right Triangles Definition And Use The Triangle Definition There Are Many Right Angle Triangles Today We Are Most Interested In Right Ppt Download
While the largest side, 2, is opposite the largest angle, 90° (TheoremAll triangles are considered special isosceles triangles The triangle has three unique properties that make it very special and unlike all the other triangles triangle ratio There are two ratios for triangles The ratio of the sides equals 1 1 2; It is a right angle triangle that complies with Pythagoras' theorem of a2b2 = c2 whereas a and b are the sides of the triangle with c being its hypotenuse What is the 30 60 90 triangle
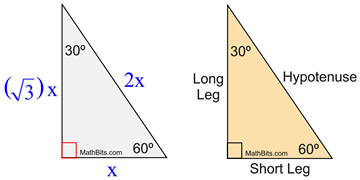



Special Right Triangle 30 60 90 Mathbitsnotebook Geo Ccss Math
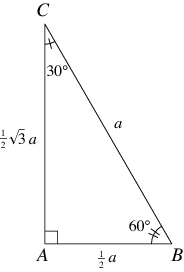



30 60 90 Triangle From Wolfram Mathworld
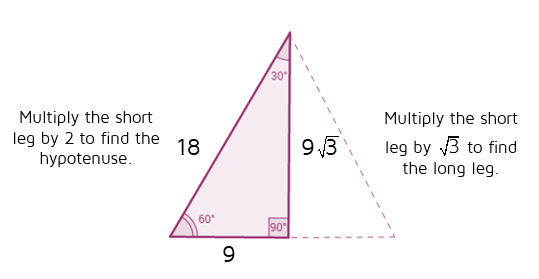
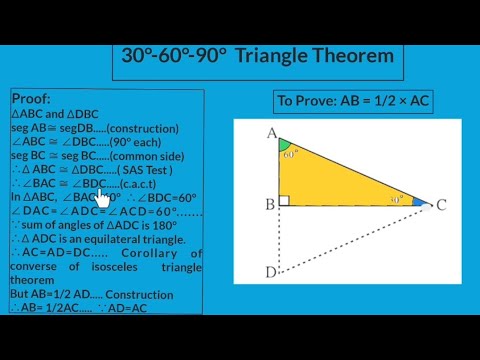
30 60 90 triangle theorem proof The proof Here is the proof that in a 30°60°90° triangle the sides are in the ratio 1 2 It is based on the fact that a 30°60°90° triangle is half of an equilateral triangle Draw the equilateral triangle ABC Then each of its equal angles is 60° (Theorems 3 and 9) A triangle8 rows A triangle is a special right triangle that always has angles of measure 30°, 60°,30 60 90 triangle rules and properties The most important rule to remember is that this special right triangle has one right angle and its sides are in an easytoremember consistent relationship with one another the ratio is a a√3 2a



1




30 60 90 Triangle Theorem Ratio Formula Video
If you add 30 to 90 you get 1 180 minus 1 leaves you with 60 degrees for that third angle Now that we know it's a 30 60 90 triangle, we can apply our 30 60 90 rules to finding the length of our ramp Our ramp is across from the 90 A 30°60°90° triangle is formed when an equilateral triangle is bisected This makes the Hypotenuse a length of x, and the short side a length of (1/2)x By the Pythagorean theorem the third side will be equal to √x² {(1/2) x}² which will equal √{4/4}x² {1/4} x² which will equal √{3/4}x² which will equal x•√(3)/2Answer (1 of 3) A triangle is special because of the relationship of its sides Hopefully, you remember that the hypotenuse in a right triangle is the longest side, which is also directly across from the 90 degree angle It turns out that in a triangle




30 60 90 Triangle Theorem Ratio Formula Video




30 60 90 Triangle Calculator Formula Rules
Special Right Triangles Formula Triangle Let's repeat the same procedure for the special right triangle {eq}30^{\circ} 60^{\circ} 90^{\circ} {/eq} Consider theThe 30°–60°–90° triangle is the only right triangle whose angles are in an arithmetic progression The proof of this fact is simple and follows on from the fact that if α , α δ , α 2 δ are the angles in the progression then the sum of the angles 3 α 3 δ = 180°A) Angle of Elevation B) Triangle Theorem C) Geometric Mean (Altitude) Theorem D) Triangle Theorem E) Geometric Mean F) Converse of The Pythagorean G) Cosine Ration H) An ehomeworkhelpercom




A Full Guide To The 30 60 90 Triangle With Formulas And Examples Owlcation



45 45 90 And 30 60 90 Triangles Zona Land Education
What is a Triangle?Special Right Triangles "Sides" "Angles" 30 6090 Right Triangle 45 45 90 Right Triangle 345 Right Triangle Others include Pythagorean theorem confirms Any multiple of 345 will work!Check out this tutorial to learn about triangles!




Special Right Triangle Wikipedia




30 60 90 Triangle Theorem Ratio Formula Video
Examples or Note Pythagorean theorem and trig relations confirm (ex sin 30 1/2 any ratio of 1 Note 5) 2 will workStart studying Triangle Theorem Learn vocabulary, terms, and more with flashcards, games, and other study toolsProperties of triangles




A Quick Guide To The 30 60 90 Degree Triangle Dummies
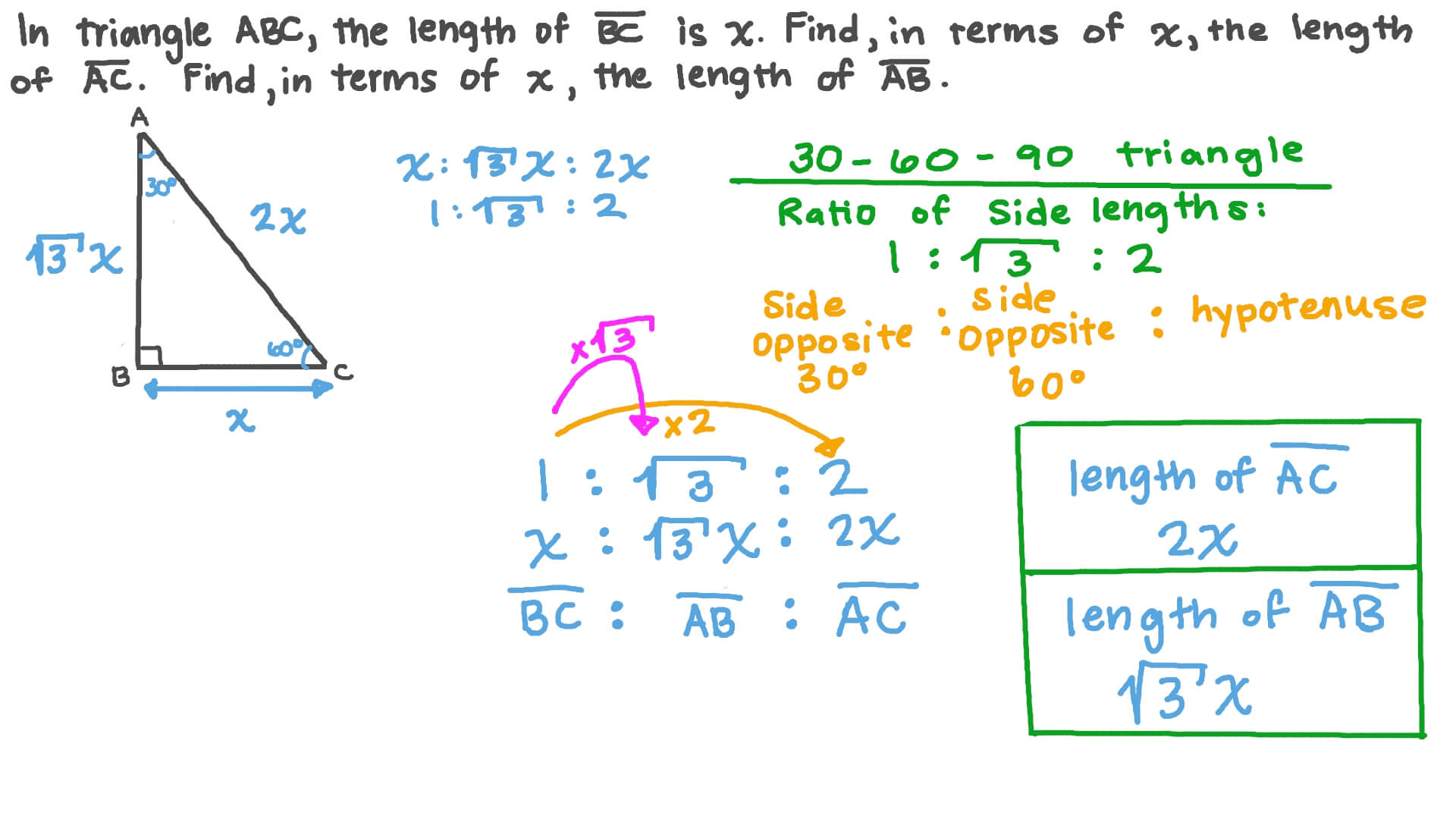



Question Video The Side Lengths Of 30 60 90 Triangles Nagwa
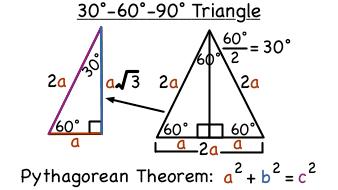
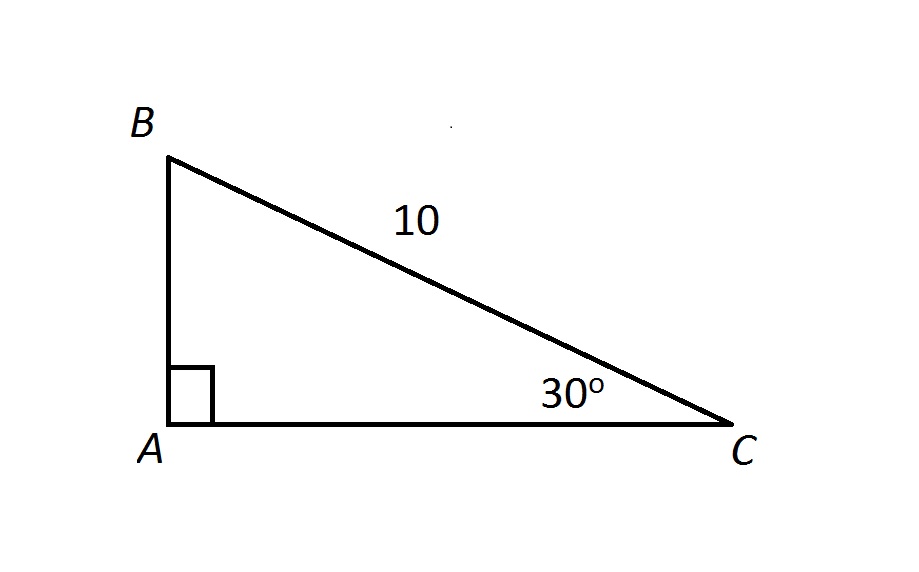
Right Triangles, Pythagorean Theorem and , DRAFT 10th 11th grade times Mathematics 70% average accuracy 2 years ago peggyrenier 0 Save Edit I have been given the short leg in this triangle How do I find the length of the hypotenuse? 👍 Correct answer to the question Which is this?Theorem In a 30°60°90° triangle the sides are in the ratio1 2 We will prove that below (For the definition of measuring angles by "degrees," see Topic 12) Note that the smallest side, 1, is opposite the smallest angle, 30°;
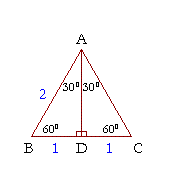



The 30 60 90 Triangle Topics In Trigonometry




30 60 90 Triangle Definition Theorem Formula Examples
Answer choices Multiply 4 by 2 Multiply 4 by √3 Multiply 4 by30 60 90 Triangle Definition Theorem Formula Examples 30 60 90 Triangles Download Ebook Special Right Triangles 30 60 90 Answers fact that if α, α δ, α 2δ are the angles in the progression then the sum of the angles 3α 3δ = 180° After dividing by 3, the angle α δ must be 60° Special right triangle Wikipedia Special right triangleThe ratio of the angles equals 1 1 2;




30 60 90 Triangles Hd Youtube




Relationships Of Sides In 30 60 90 Right Triangles Ck 12 Foundation




30 60 90 Right Triangles Ck 12 Foundation




A Full Guide To The 30 60 90 Triangle With Formulas And Examples Owlcation




30 60 90 Right Triangle Side Ratios Expii



1




30 60 90 Triangles



5 5 Special Triangles




A Quick Guide To The 30 60 90 Degree Triangle Dummies
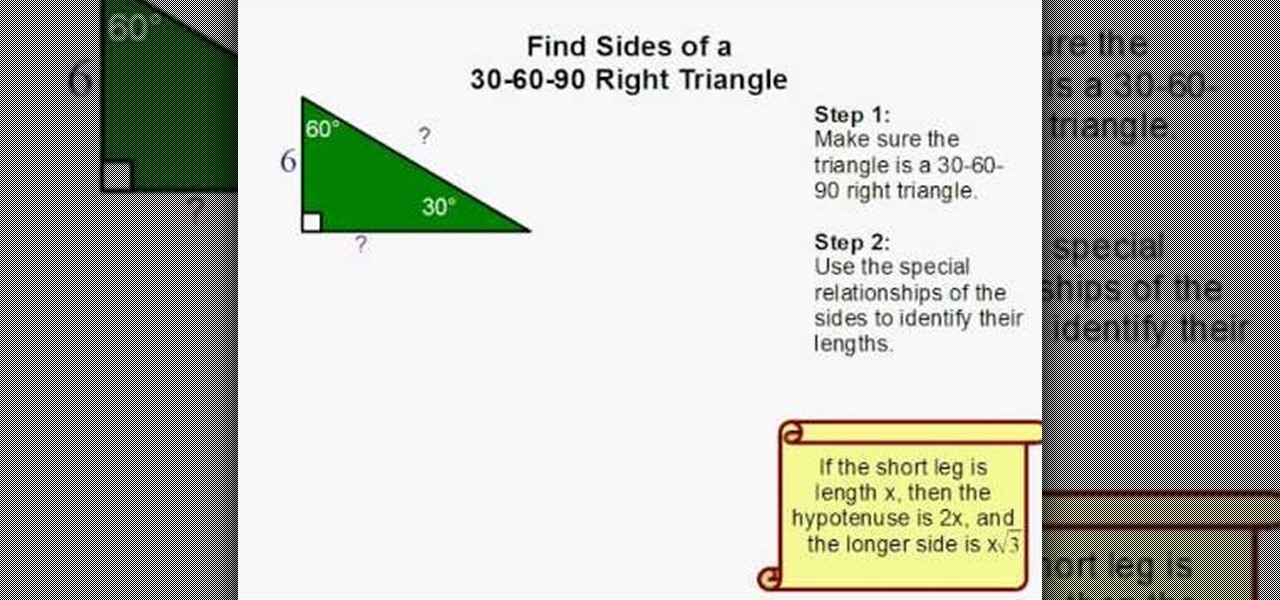



How To Find The Sides Of A 30 60 90 Right Triangle Math Wonderhowto




The Complete Guide To The 30 60 90 Triangle
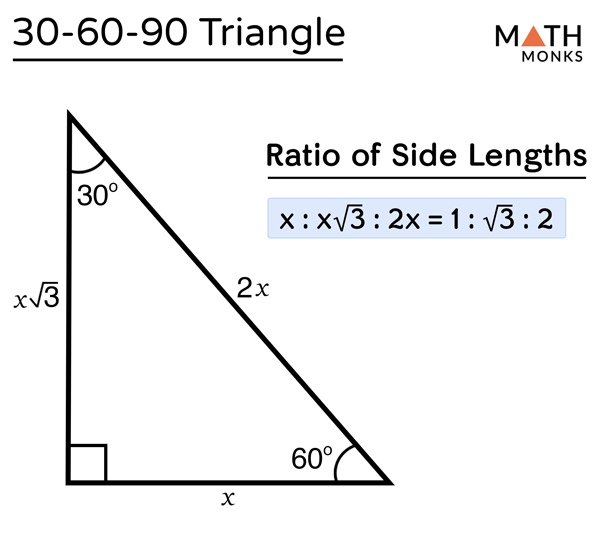



30 60 90 Triangle Definition Formulas Examples




Special Right Triangles Definition And Use The Triangle Definition There Are Many Right Angle Triangles Today We Are Most Interested In Right Ppt Download




A Full Guide To The 30 60 90 Triangle With Formulas And Examples Owlcation
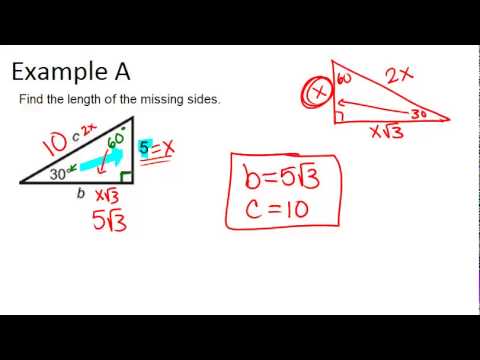



30 60 90 Right Triangles Examples Geometry Concepts Youtube




Special Right Triangles Review Article Khan Academy




Right Triangles 30 60 90 Special Right Triangles Notes And Practice
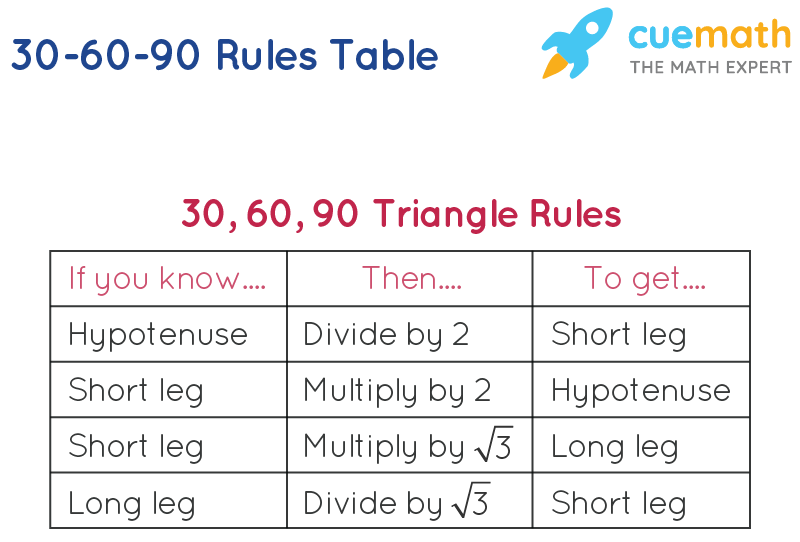



30 60 90 Formula Learn Formula For Calculating The 30 60 90 Measures




30 60 90 Triangle Explanation Examples
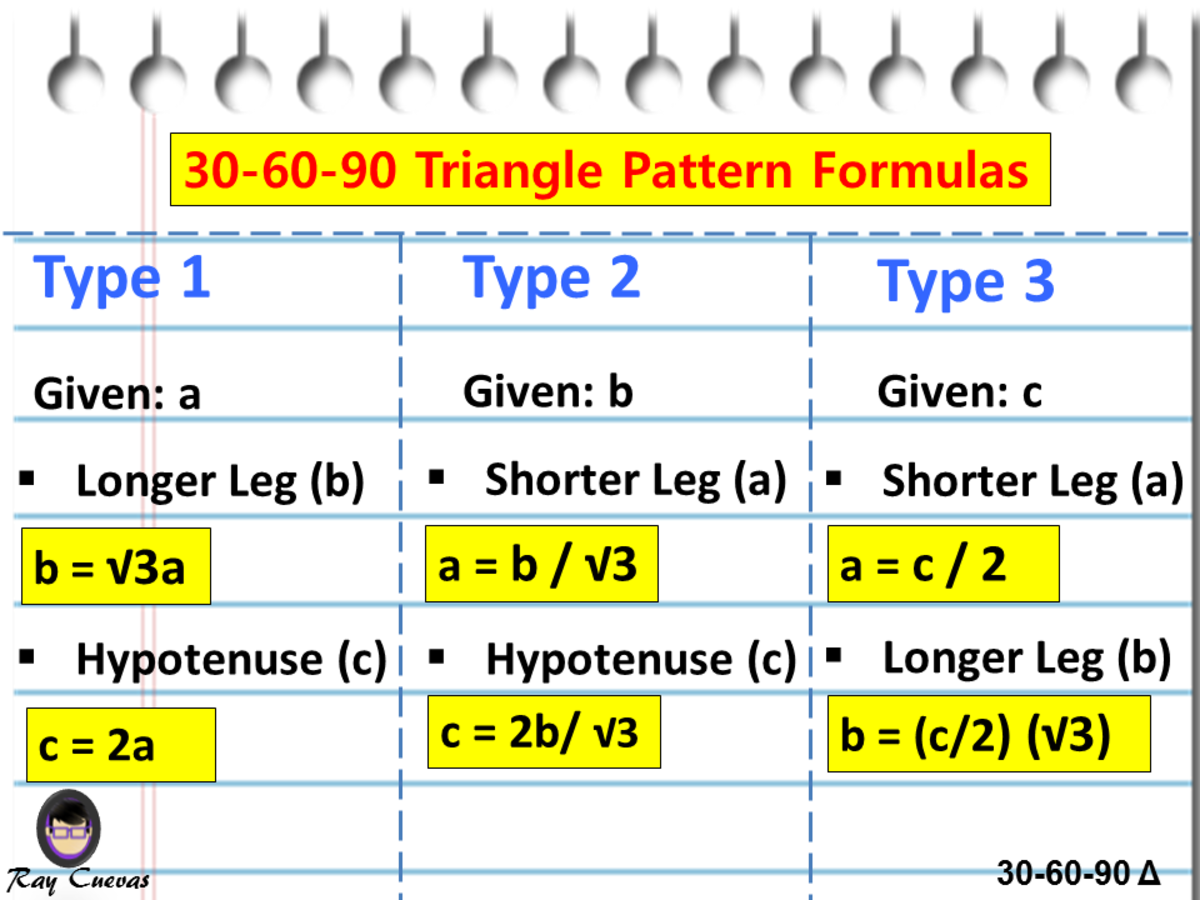



A Full Guide To The 30 60 90 Triangle With Formulas And Examples Owlcation




Special Right Triangles Video Lessons Examples And Solutions
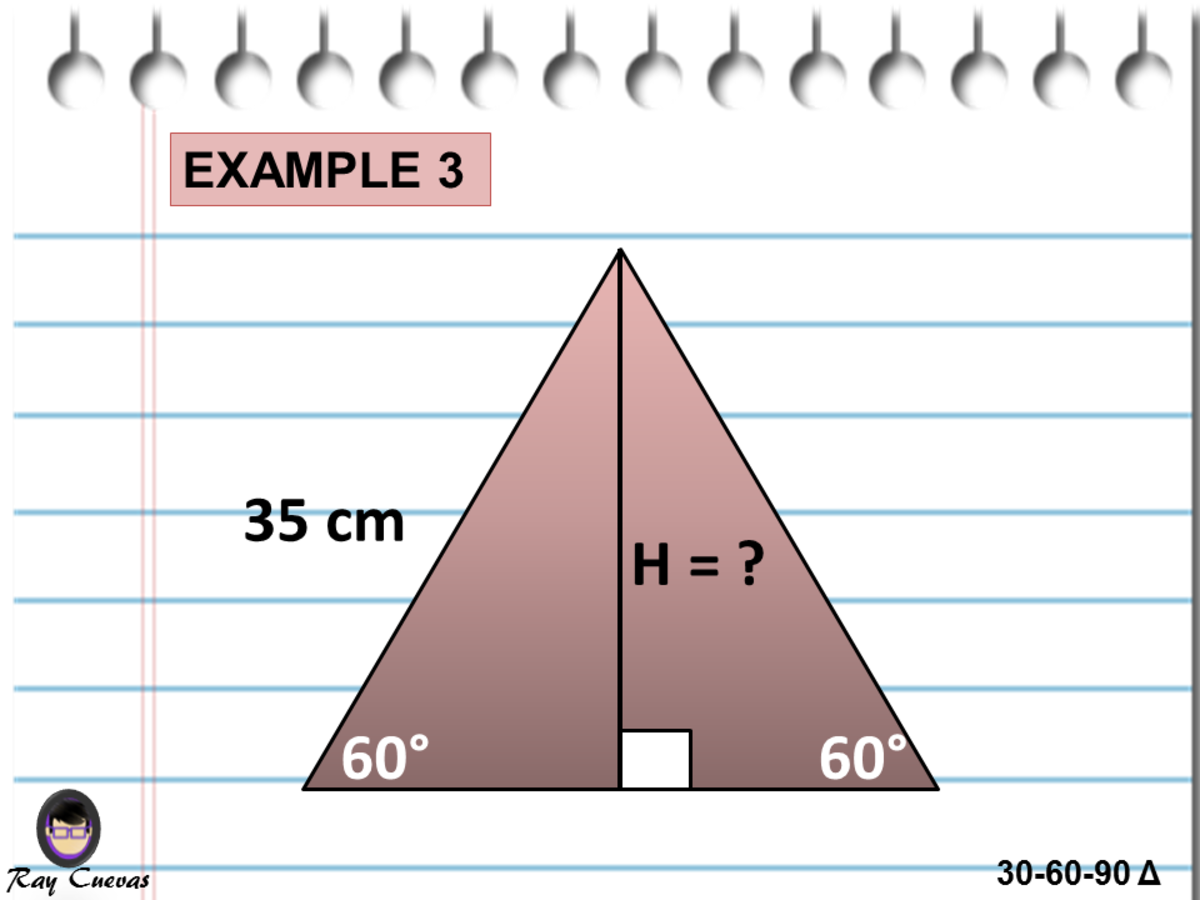



A Full Guide To The 30 60 90 Triangle With Formulas And Examples Owlcation
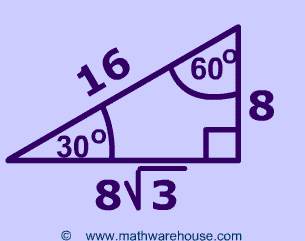



Fastest What Is The Rule For A 30 60 90 Triangle



What Are Some Differences And Similarities Between 30 60 90 Triangles And 45 45 90 Triangle Quora




30 60 90 Triangle Definition Theorem Formula Examples



3



What Are The Side Ratios For A 30 60 90 Triangle Quora




Special Right Triangles Fully Explained W 19 Examples




30 60 90 Triangle Theorem Ratio Formula Video




The Complete Guide To The 30 60 90 Triangle



30 60 90 Triangle Rules




30 60 90 Triangle Definition Theorem Formula Examples




30 60 90 Triangle Theorem Ratio Formula Video
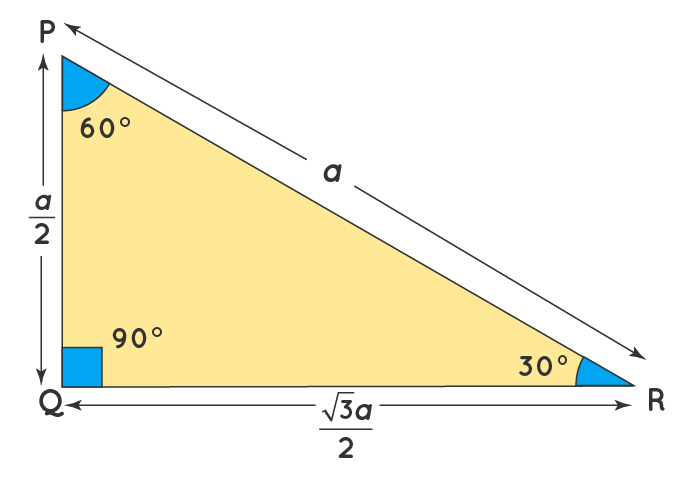



30 60 90 Triangle Definition Theorem Formula Examples
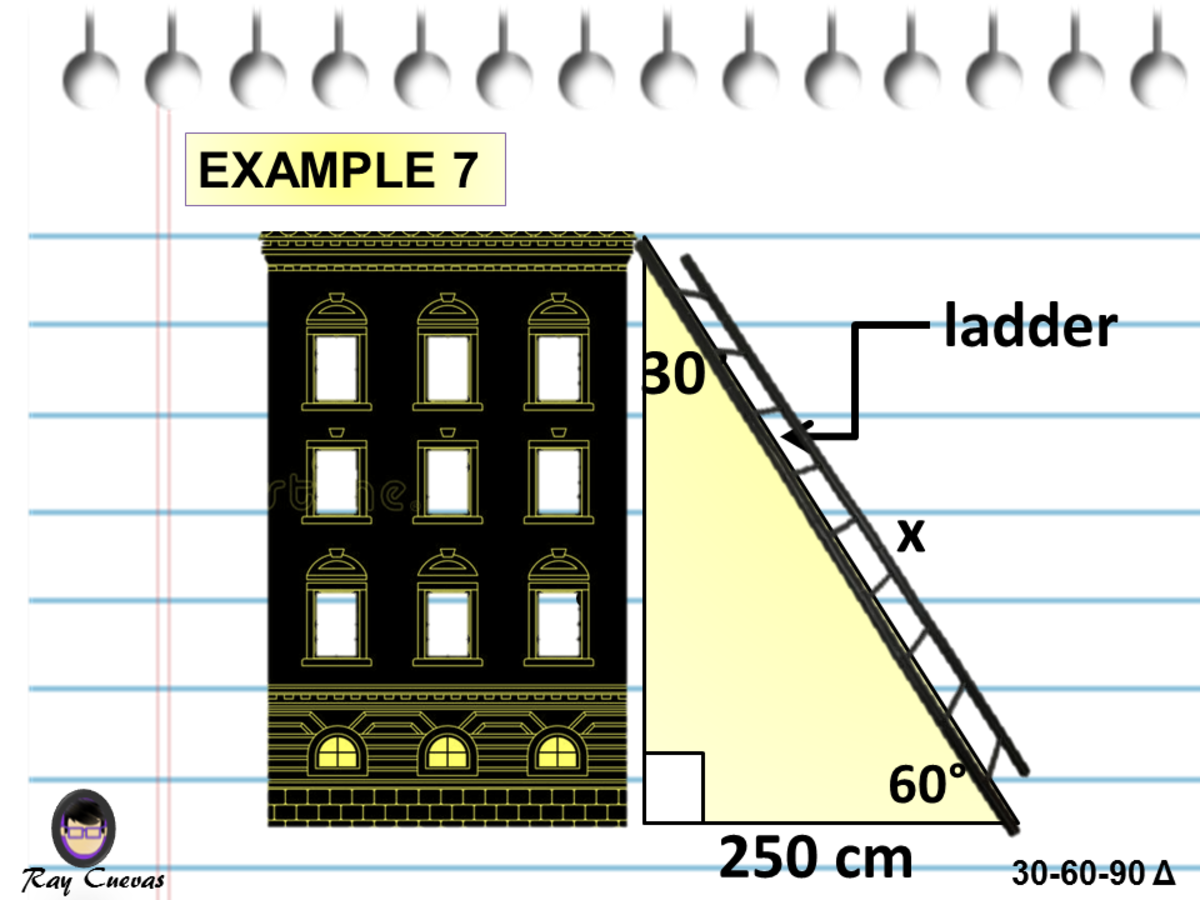



Fastest What Is The Rule For A 30 60 90 Triangle



The Easy Guide To The 30 60 90 Triangle




30 60 90 Triangles




Geometry Proofs Math 416 Time Frame N N
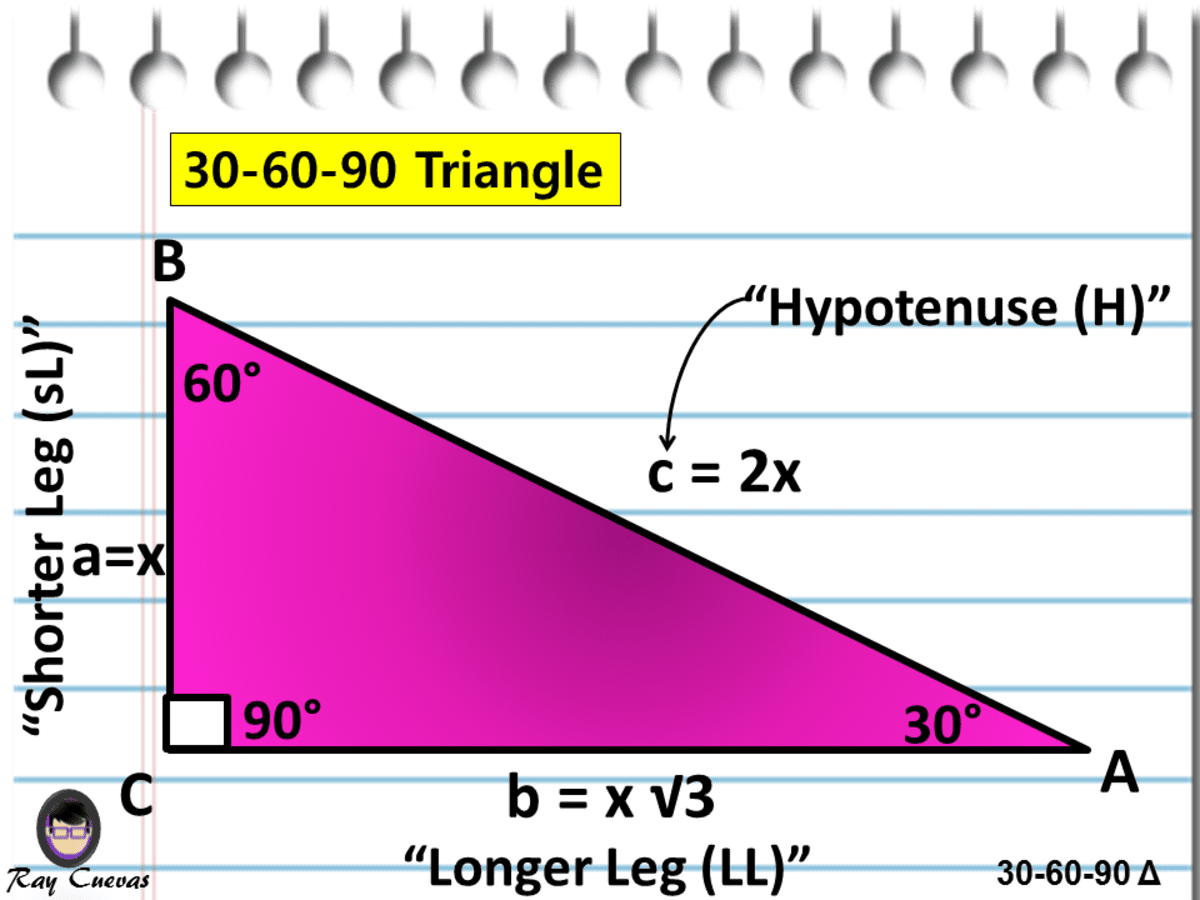



A Full Guide To The 30 60 90 Triangle With Formulas And Examples Owlcation



What Is A 30 60 90 Degree Triangle Virtual Nerd




30 60 90 Triangle Definition Math Open Reference




30 60 90 Triangle Explanation Examples



A Full Guide To The 30 60 90 Triangle With Formulas And Examples Owlcation



Special Triangles Hiset Math



30 60 90 Triangles P4 Kate S Math Lessons



1



9th Maths 2 30 60 90 Triangle Theorem Youtube




30 60 90 Triangle Theorem Proof Don T Memorise Youtube
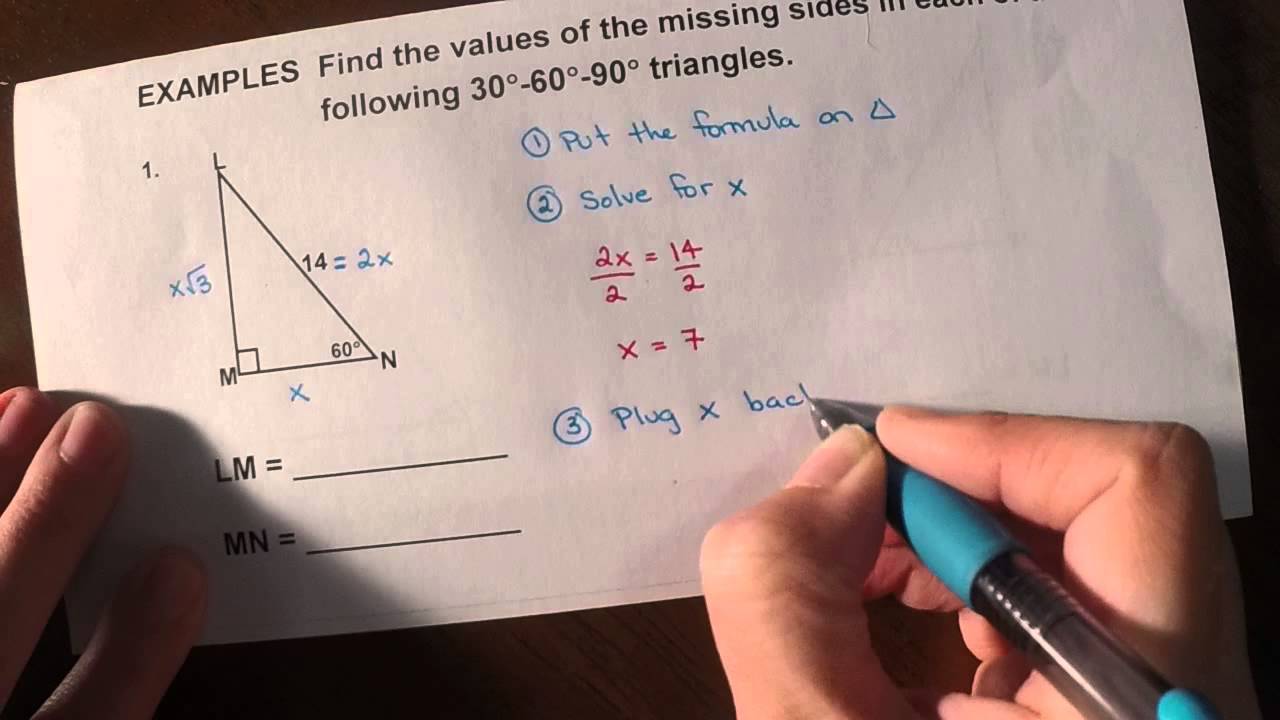



30 60 90 Triangles Youtube
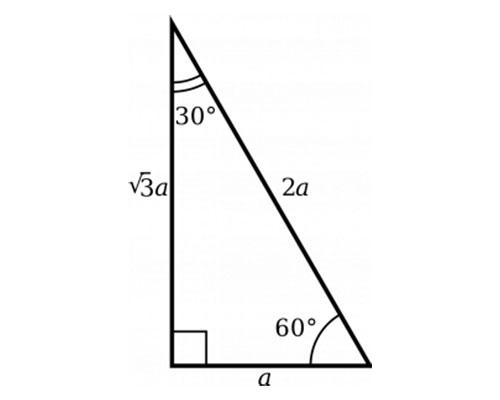



30 60 90 Triangle Sides Examples Angles Full Lesson



The Easy Guide To The 30 60 90 Triangle




30 60 90 Triangle Theorem Properties Formula Video Lesson Transcript Study Com



Mrwadeturner 30 60 90 Triangle 6th
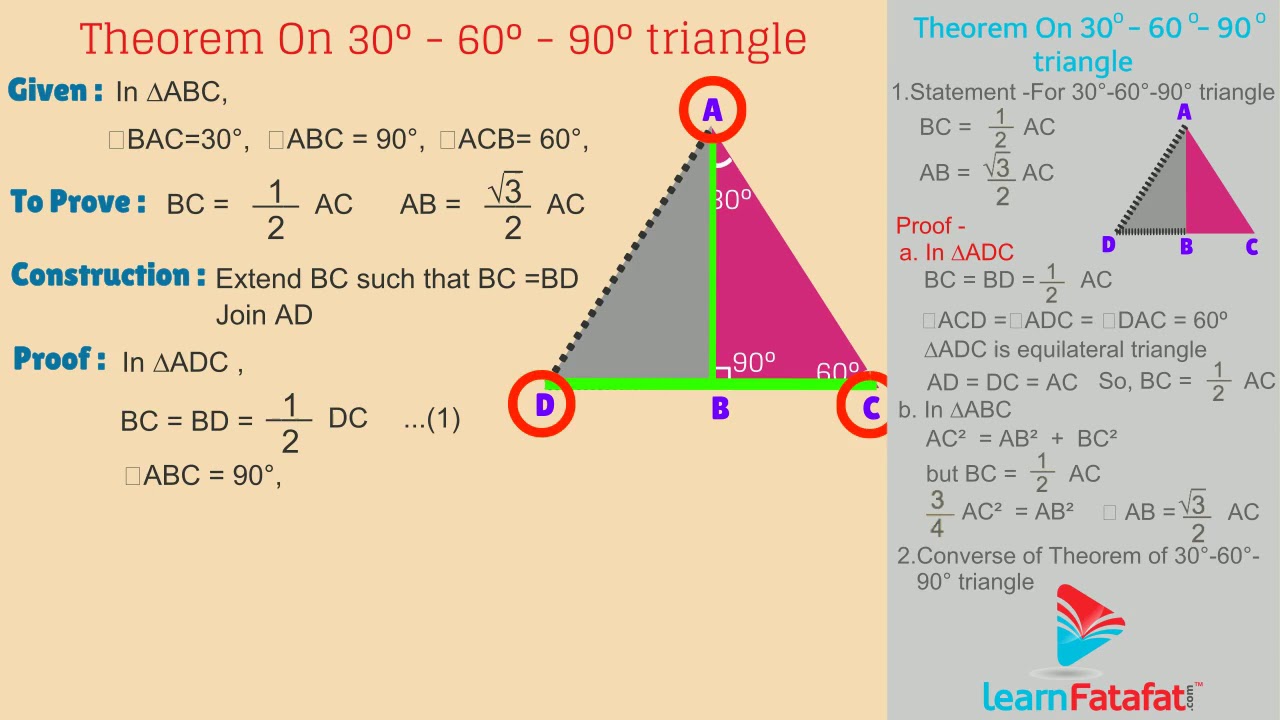



Pythagoras Theorem On 30 60 90 Triangle Youtube




30 60 90 Right Triangles Ck 12 Foundation




30 60 90 Triangle Theorem Ratio Formula Video




30 60 90 Triangle Theorem Ratio Formula Video




Foundation Class X Theorem Of 30 60 90 Triangle In Marathi Offered By Unacademy



Special Right Triangles




Right Triangles 30 60 90 Special Right Triangles Notes And Practice




30 60 90 Right Triangles Ck 12 Foundation




30 60 90 Triangle Theorem Properties Formula Video Lesson Transcript Study Com
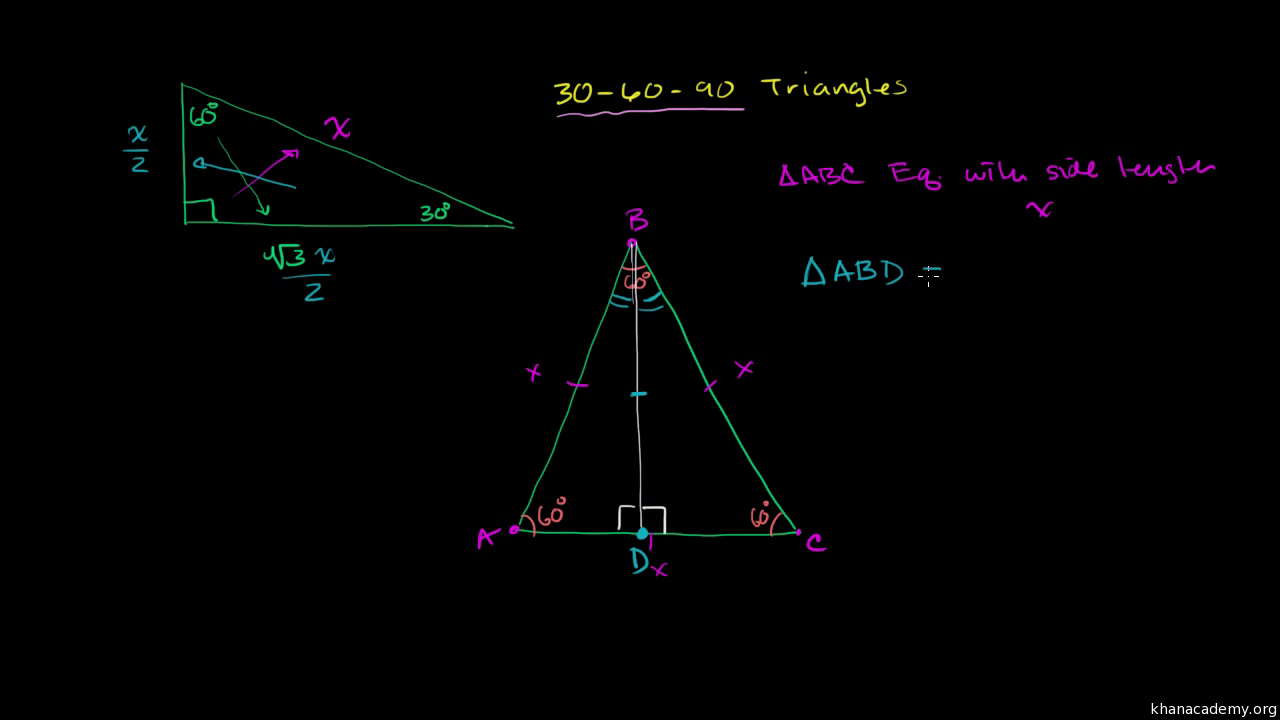



Special Right Triangles Proof Part 1 Video Khan Academy
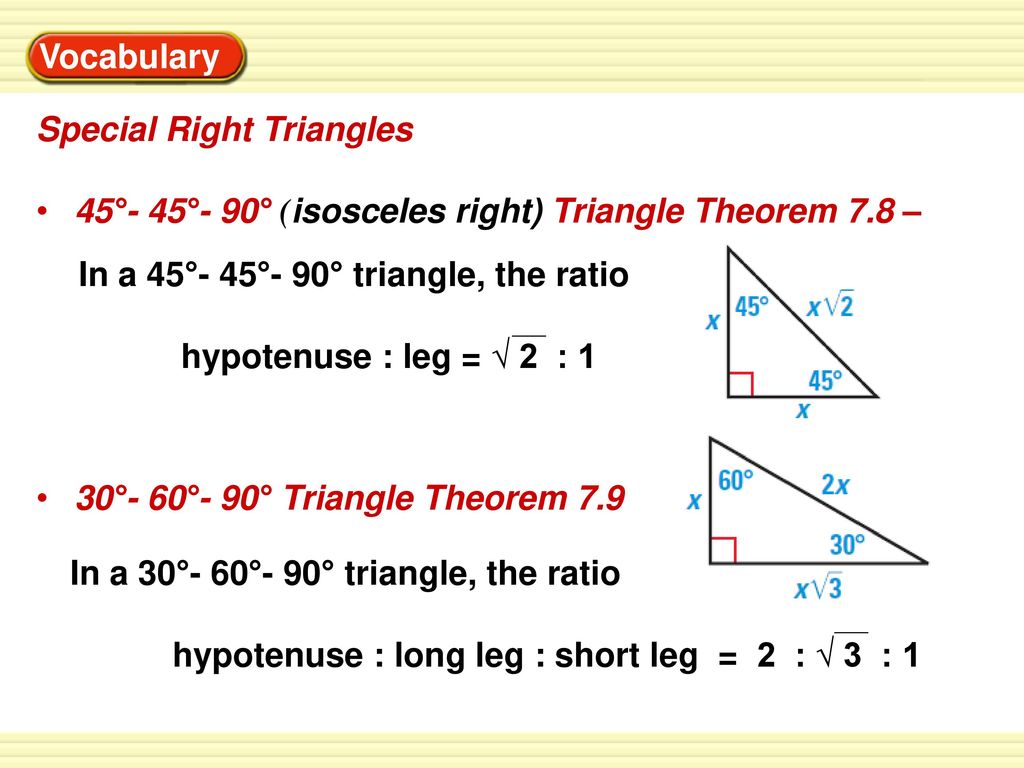



Simplify Answer Answer 12 Answer Ppt Download




Learn About The 30 60 90 Triangle Caddell Prep Online
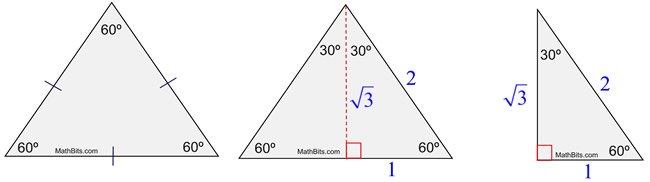



Special Right Triangle 30 60 90 Mathbitsnotebook Geo Ccss Math




How To Work With 30 60 90 Degree Triangles Education Is Around




30 60 90 Triangle Calculator Formula Rules



The Easy Guide To The 30 60 90 Triangle
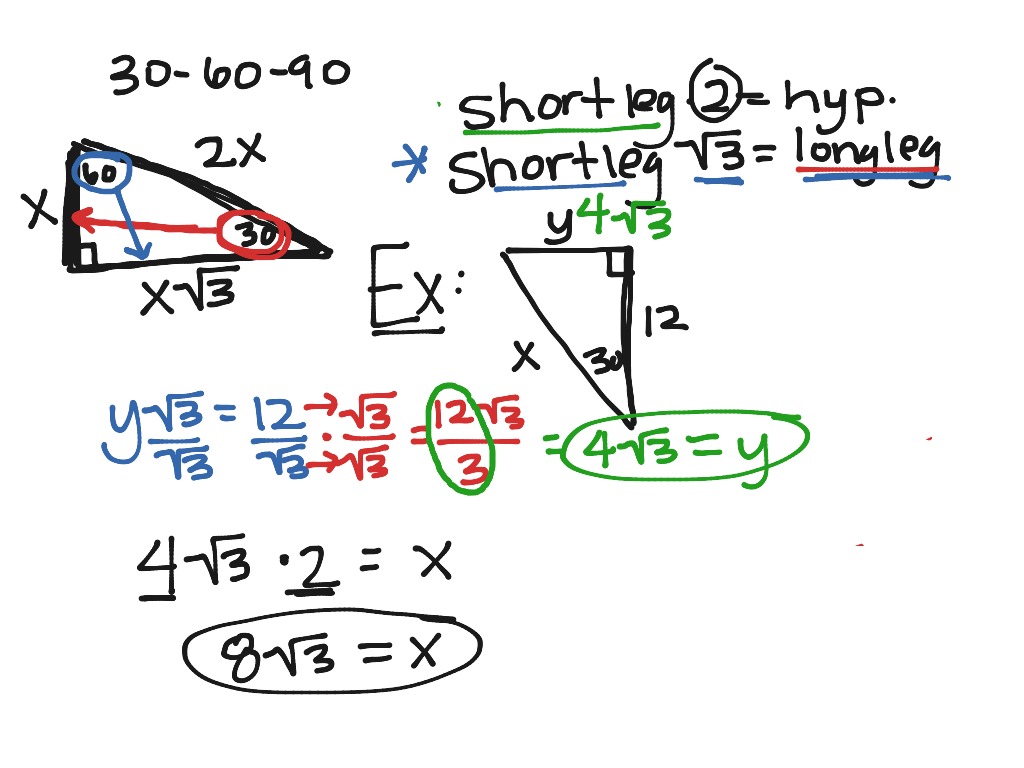



30 60 90 Triangle Examples Math Geometry Showme




30 60 90 Triangle Theorem Properties Formula Video Lesson Transcript Study Com




5 30 60 90 Triangles Geometry15a




30 60 90 Triangle Theorem Ratio Formula Video




30 60 90 Triangle Example Problem Video Khan Academy
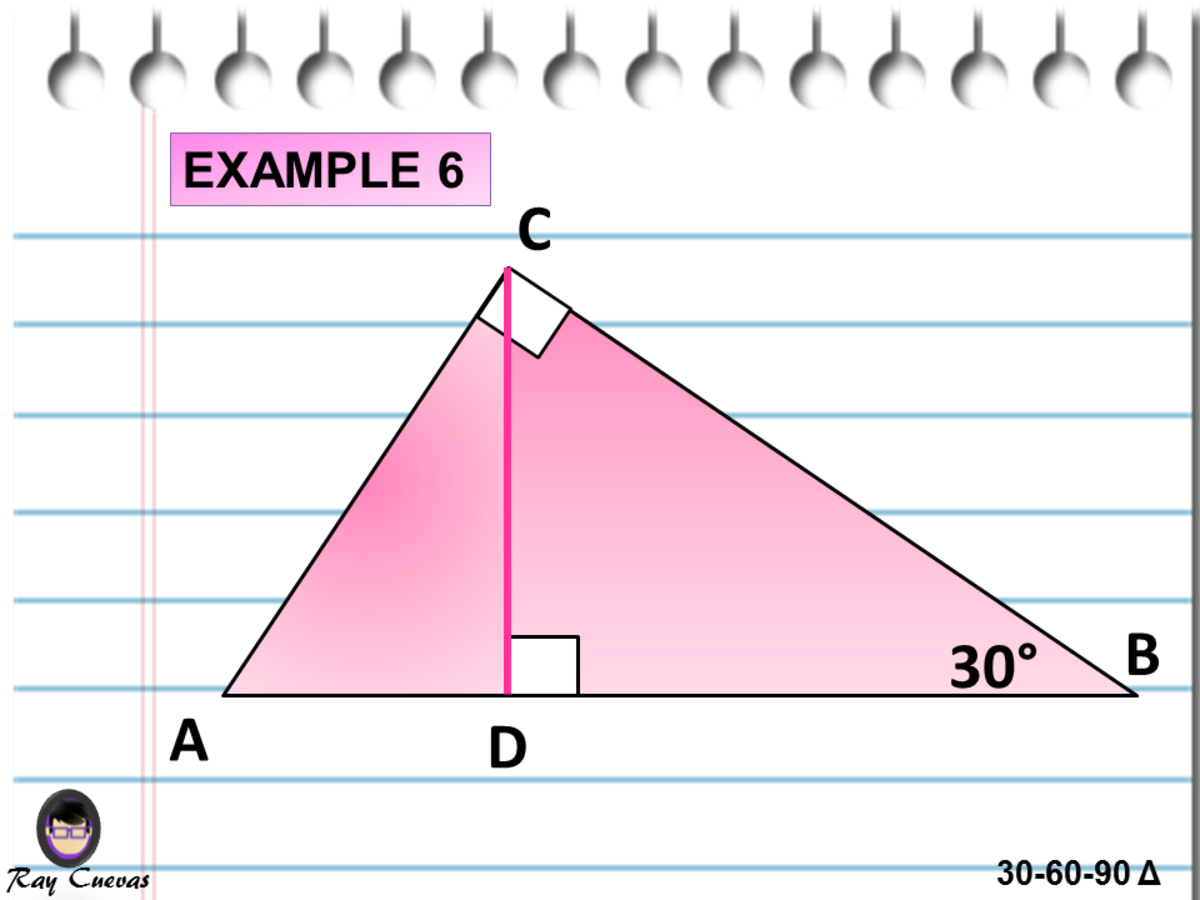



Fastest What Is The Rule For A 30 60 90 Triangle




30 60 90 Right Triangles Ck 12 Foundation




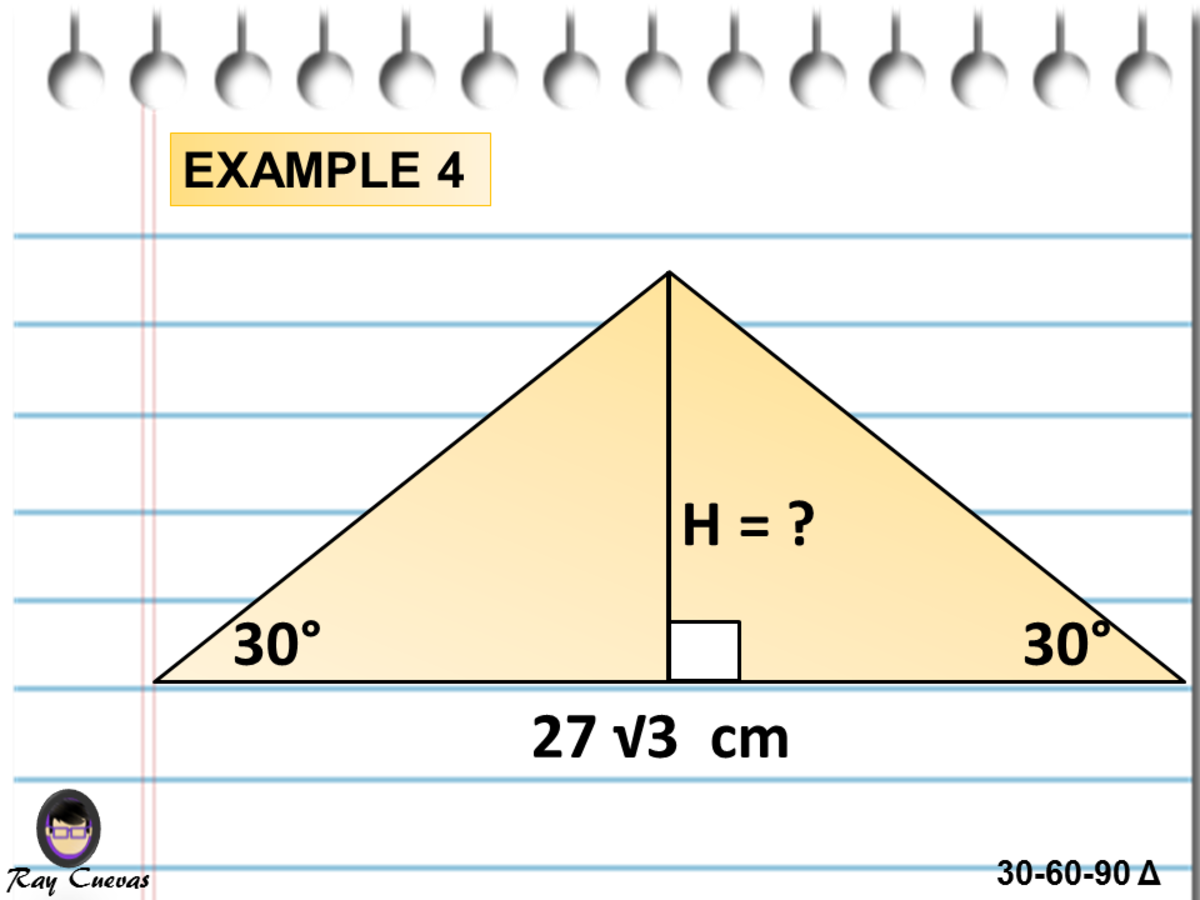
Example 4 Find The Height Of An Equilateral
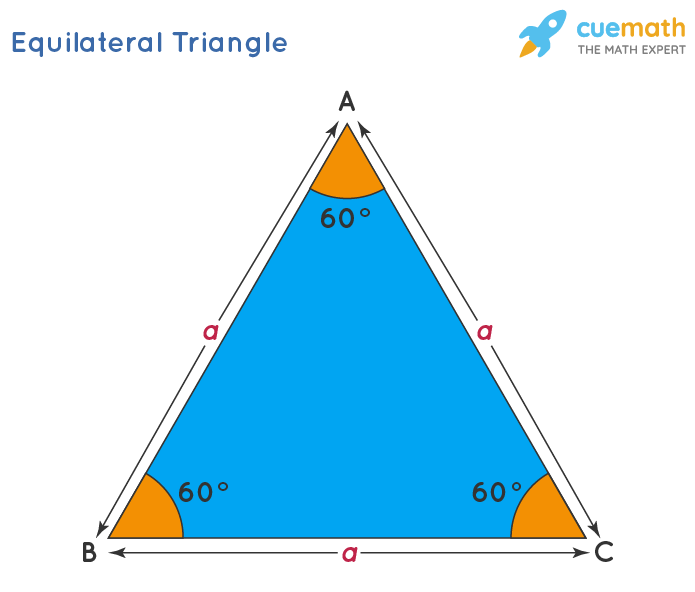



30 60 90 Triangle Definition Theorem Formula Examples
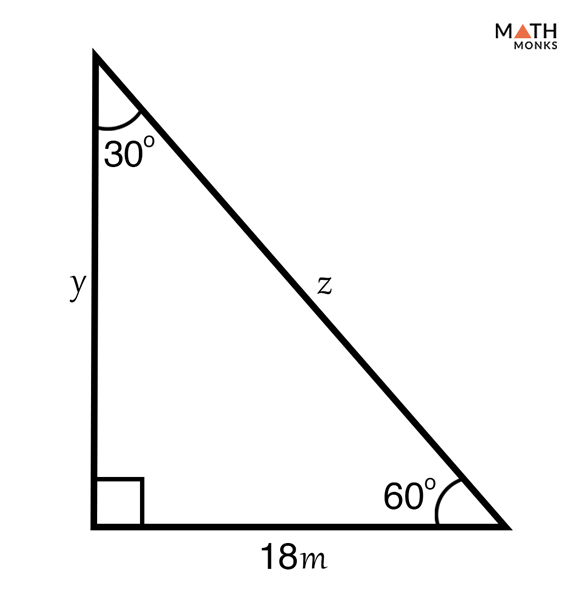



30 60 90 Triangle Definition Formulas Examples



Mrwadeturner 30 60 90 Triangle 6th



The Easy Guide To The 30 60 90 Triangle




30 60 90 Right Triangles Lesson Geometry Concepts Youtube




The 30 60 90 Triangle Topics In Trigonometry
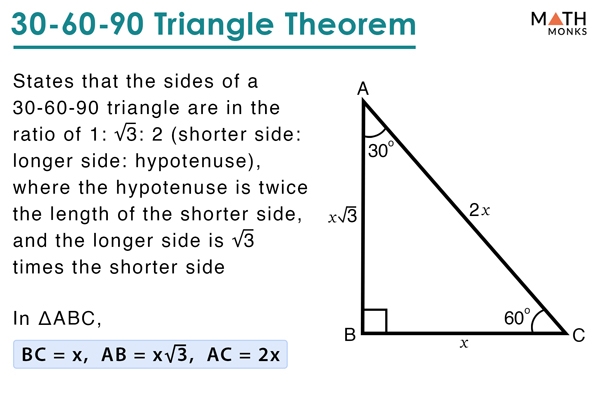



30 60 90 Triangle Definition Formulas Examples




30 60 90 Right Triangles Solutions Examples Videos




Special Right Triangles Interactive Notebook Page Math Methods Teaching Geometry Teaching Math



0 件のコメント:
コメントを投稿